1.K近邻算法原理
K近邻算法原理就是给出一个点a,然后将找出离点a距离最近的k个点所属的类别。然后a的类别就属于k个点中所属类别最多的那个类。
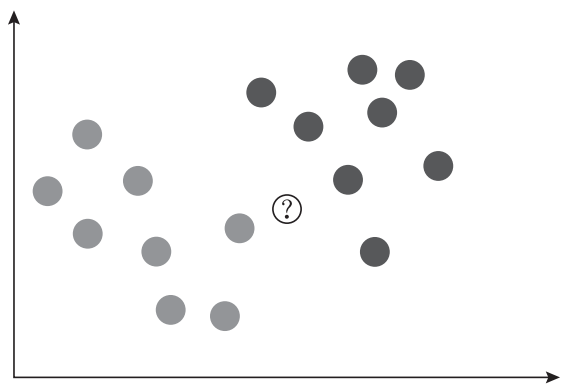
比如下图,总共选取距离a点最近的3个点(k = 3)。深色的类别占2个点,浅色的类占1个点,所以a点属于深色类。
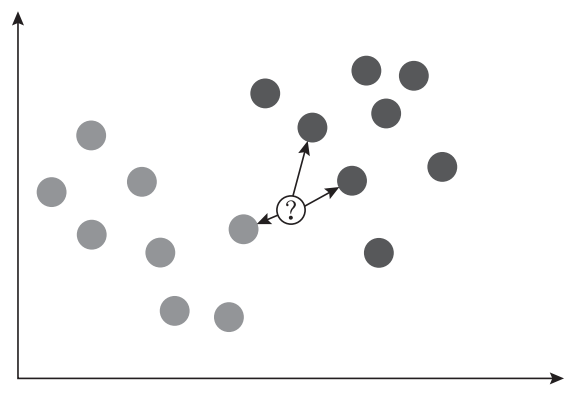
以上就是 K 最近邻算法在分类任务中的基本原理,实际上 K 这个字母的含义就是最近邻的个数。
KNN的工作原理大致分为三步:
- 计算待分类物体与其他物体之间的距离;
- 统计距离最近的 K 个邻居;
- 对于 K 个最近的邻居,它们属于哪个分类最多,待分类物体就属于哪一类。
K最近算法也可以用于回归,原理和其用于分类是相同的。 当我们使用 K 最近邻回归计算某个数据点的预测值时,模型会选择离该数据点最近的若干个训练数据集中的点, 并且将它们的 y 值取平均值,并把该平均值作为新数据点的预测值。
根据KNN的工作原理,有两个问题需要进行解决
- 怎样确定这个点与相近点之间的距离
- 怎样确定k值。
距离计算
在机器学习中,通常使用欧式距离计算比较多通过计算所给点与所有点之间的距离,可以很容易找出与所给点最近的几个点。
其他计算距离的公式诸如“曼哈顿距离”、“闵可夫斯基距离”、“切比雪夫距离”、“余弦距离”等不详细展开了,有兴趣可以自行了解。
k的取值
选取正确的k值对于整个模型的正确率影像很大,但k值无法靠先验知识进行设置需要不断的尝试。 工程上,我们一般采用交叉验证的方式选取K值。
交叉验证的思路就是,把样本集中的大部分样本作为训练集,剩余的小部分样本用于预测,来验证分类模型的准确性。所以在 KNN 算法中,我们一般会把 K 值选取在较小的范围内,同时在验证集上准确率最高的那一个最终确定作为 K 值。
在k取值过程中如果 K 值比较小,就相当于未分类物体与它的邻居非常接近才行。这样产生的一个问题就是,如果邻居点是个噪声点,那么未分类物体的分类也会产生误差,这样 KNN 分类就会产生过拟合。
如果 K 值比较大,相当于距离过远的点也会对未知物体的分类产生影响,虽然这种情况的好处是鲁棒性强,但是不足也很明显,会产生欠拟合情况,也就是没有把未分类物体真正分类出来。
在sklearn的模型中k值默认为5。
2. 在sklearn中使用KNN
我们使用手写数字数据集作为此次训练的数据集。这个数据集是非常有名的用于图像识别的数据集。完整的手写数字数据集 MNIST 里面包括了 60000 个训练样本,以及 10000 个测试样本。数据集中每一张图片为0-9中的单个数字。
我们用 sklearn 自带的手写数字数据集做 KNN 分类,这个数据集只包括了 1797 幅数字图像,每幅图像大小是 8*8 像素。
整个训练过程基本上包括四个阶段:
- 数据加载:我们可以直接从 sklearn 中加载自带的手写数字数据集,或者从外部加载读取数据集,本次我们使用自带的手写数据集。
- 数据预处理:通过数据预处理可以让数据都在同一个维度。此外,因为训练集是图像,每幅图像是个 8x8 的矩阵,我们不需要对它进行特征选择,将全部的图像数据作为特征值矩阵即可;
- 模型训练:将训练图片与标签”喂”给算法,然后得到训练好的模型。
- 模型评估:使用测试集对训练好的模型进行准确率的计算。
好了,下面我们开始吧:
首先,导入包,这里导入了很多算法包,是因为既然这次项目比较简单,都那么我们就对比一下之前的几种方法,看看效果。
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.datasets import load_digits
from sklearn.preprocessing import MinMaxScaler, StandardScaler
from sklearn.model_selection import train_test_split
from sklearn.neighbors import KNeighborsClassifier
from sklearn.metrics import accuracy_score
#加载数据
digits = load_digits()
data = digits.data
target = digits.target
print(data.shape)
#打印第一张图像
print(digits.images[0])
#打印第一张图片标签(label)
print(target[0])
#将第一幅图像显示出来
plt.gray()
plt.imshow(digits.images[0])
plt.show()
结果如下:
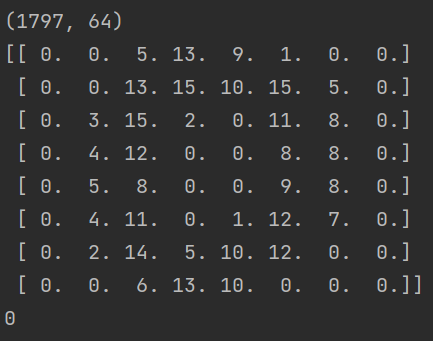
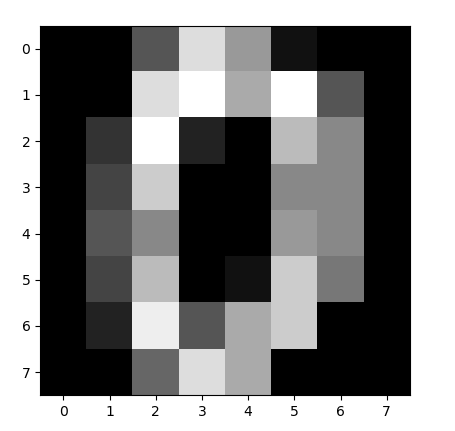
可以看到第一张图片0是由8x8像素组成的矩阵。
接着我们需要将所有的数据集划分为训练集与测试集。一般按照8-2分。
train_x, test_x, train_y, test_y = train_test_split(data1, target1, test_size=0.25)
划分完毕后,使用z-score、0-1归一化的方式进行数据预处理。
#采用z-score规范化
ss = StandardScaler()
train_ss_scaled = ss.fit_transform(train_x)
test_ss_scaled = ss.transform(test_x)
#采用0-1归一化
mm = MinMaxScaler()
train_mm_scaled = mm.fit_transform(train_x)
test_mm_scaled = mm.transform(test_x)
首先使用Z-Score 会将数值规范化为一个标准的正态分布,即均值为 0,方差为 1。 因为KNN需要度量距离,一般在特征值差距较大时,都会进行归一化/标准化,不然会出现样本计算不均衡的问题。我们在此处使用归一化进行数据预处理。
模型训练
models = KNeighborsClassifier()
model.fit(train_ss_scaled, train_y)
模型预测
predict = model.predict(test_ss_scaled)
print(model_key, "准确率: ", accuracy_score(test_y, predict))
输出结果:
KNN 准确率: 0.9644444444444444
3. 小结
在本章中,我们介绍了 K 最近邻算法的原理和它的使用方法, K 最近邻算法可以说是一个非常经典而且原理十分容易理解的算法。不过 K 最近邻算法在实际使用当中会有很多问题,例如它需要对数据集认真地进行预处理、对规模超大的数据集拟合的时间较长、对高维数据集拟合欠佳,以及对于稀疏数据集束手无策等。 所以在当前的各种常见的应用场景中,K 最近邻算法的使用并不多见。
本篇主要内容来自 https://zhuanlan.zhihu.com/p/122537207